0. 목표
자바의 Class에 대해서 학습한다.
-
학습할 것(필수)
- (클래스란?)
- 클래스를 정의하는 방법
- 객체를 만드는 방법 (new 연산자 이해하기)
- 메소드를 정의하는 방법
- 생성자를 정의하는 방법
- this란 무엇인가? this. 와 this()
-
학습할 것(추가)
- (이진트리란?)
- 이진트리 구현하기
- 이진탐색트리 구현하기
- (추가)contains(int number) 구현
- (추가)remove(int number) 구현
-
Plus Ultra
- 이진 트리의 활용
- 균형 이진 탐색트리
- AVL 트리
- Red - Black 트리
- 힙
- 균형 이진 탐색트리
- 이진 트리의 활용
1. 클래스란?
내가 원하는 작업을 수행 할 함수, 프로시져, (작업을 진행하는데 필요한) 변수들을 한군데에 모아서 인지하기 쉽도록 만든것
2. 클래스를 정의하는 방법
Place.java
class Place {
}- 위와 같이 Place.java 소스파일에
class라는 단어를 작성하고 클래스의 이름을 짓고 괄호를 열고 닫으면 클래스가 정의된다. - 네이밍 컨벤션
- 클래스의 이름은 명사이어야 한다.
ex) Place (o) , Change (x) - 각 단어의 첫글자는 대문자로한다.(파스칼 케이스)
ex) PlaceCalulator (o) , placeCalculator (x) , Placecalculator (x) , placecalculator(x) - 이니셜등 축약어는 잘 알려진 축약어가 아니라면 피한다.
ex) PlaceCalculator (o) , PlaceCCL (x)
- 클래스의 이름은 명사이어야 한다.
- 클래스 내부에 변수를 선언할 수 있다.
- 의외로 파일의 이름과 클래스 이름은 다르게 지어도 된다. 사실 잘 몰랐는데 심심해서 해봤는데 됐다. 동일 패키지 내부에 있다면 찾을 수 있다.
- 다만 해당 클래스파일을 외부 패키지에서 사용할 수 있게 하기 위해서는 public 접근제어자를 앞에 붙여야 하는데 public 접근제어자가 붙는 클래스는 파일과 이름이 동일해야한다.
- 한 소스코드 내부에 public class는 하나만 존재한다. 아래 코드로 확인해보자.
Dog.java
package study.moon.test;
class Word {//Dog.java파일에 Word클래스를 정의했는데 컴파일에러가 없다.
char[] character;
}더 재미있는건 이 경우에 Dog.java 파일을 컴파일했는데 Word.class파일만 생성된다.

Main1.java
package study.moon.test;
public class Main1 {
public static void main(String[] args) {
Word word = new Word(); //동일한 패키지에 있다면 Word.java라는 파일이 없어도 인스턴스 생성이 가능하다.
word.character = new char[]{'H','E','L','L','O'};
System.out.print(word.character); // HELLO
}
}Main2.java -> 컴파일 에러
package study.moon.test2;//다른 패키지
import study.moon.test.Word;
public class Main2 {
public static void main(String[] args) {
Word word = new Word();
}
}Dog.java -> 컴파일 에러
package study.moon.test;
class Dog {
Word name;
}
public class Word {//파일 이름과 클래스 이름이 다름
char[] character;
}Dog.java -> 컴파일 에러
package study.moon.test;
public class Dog {
Word name;
}
public class Word {//한 소스코드에 public 클래스가 2개임
char[] character;
}2. 객체를 만드는 방법
Main.java
package study.moon.test;
public class Main {
public static void main(String[] args) {
Animal animal = new Animal();
}
}Animal.java
public class Animal {
String name;
Place place;
}- new 연산자는 heap영역에 메모리를 할당하고, 할당한 메모리의 주소를 반환하는 연산자이다.
- 위와 같이 변수를 선언하고 new연산자를 사용한 후 new 연산자 뒤에 해당 클래스의 생성자 메소드를 호출하여 객체를 생성하고 선언해뒀던 변수에 참조값을 대입하여 변수를 초기화한다.
- 해당 클래스에 생성자메소드가 없으면 아무런 매개변수도 없는 생성자 메소드가 자동으로 생성된다.
Animal.class
public class study.moon.test.Animal {
java.lang.String name;
study.moon.test.Place place;
public study.moon.test.Animal();
Code:
0: aload_0
1: invokespecial #1 // Method java/lang/Object."<init>":()V <---생성자를 만든적이 없는데 생겼다.
4: return
}3. 메소드를 정의하는 방법
Place.java
package study.moon.test;
class Place {
int latitude;
int longitude;
int altitude;
public void changePlace(int latitude, int longitude, int altitude) {//메소드 정의
this.latitude += latitude;
this.longitude += longitude;
this.altitude += altitude;
}
}-
제일 앞에 제어자를 붙이고 반환형을 붙인다. 그 후 메소드명을 정하고 괄호 안에 매개변수를 입력한 후 괄호를 연다. 그리고 반환형에 맞는 return값을 반환한다.
ex)제어자 반환형 메소드명 (매개변수...) { return 반환형; } -
메소드의 내부에는 자신이 원하는 로직을 작성할 수 있다.
-
네이밍 컨벤션
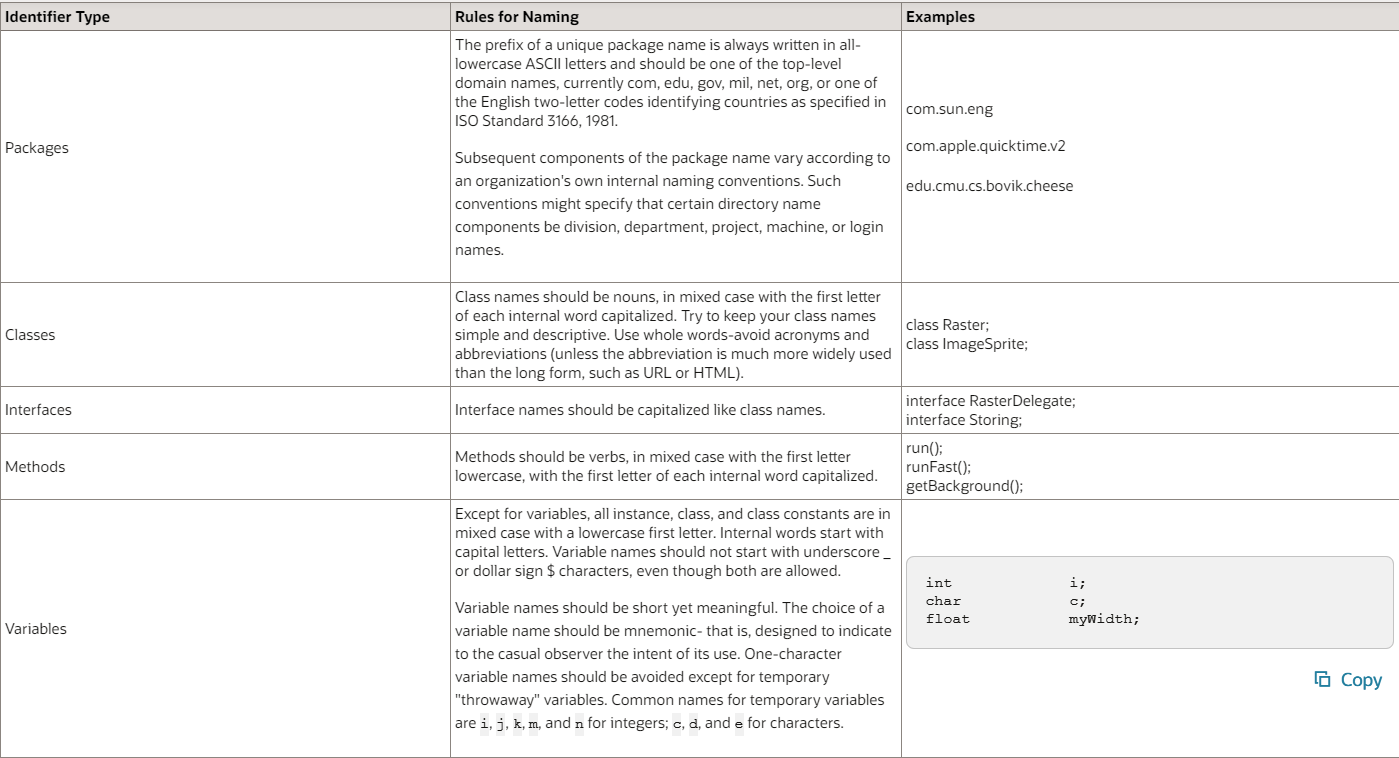
-
메소드의 이름은 동사를 포함해야한다.
ex) apple (x) , changeColor (o) -
각 단어의 첫글자는 소문자로, 나머지는 대문자로한다.(카멜 케이스)
ex) computeCoordinate (o), coordinatecalculate (x) -
자바 코딩 컨벤션은 회사마다 조금씩 다르게 사용하지만 대체적으로 거의 비슷하니 일반적으로 사용하는 컨벤션들은 외워두는것이 좋다.
4. 생성자를 정의하는 방법
생성자란?
생성자는 new 연산자로 생성된 객체의 초기화를 담당한다.
Place.java
package study.moon.test;
class Place {
int latitude;
int longitude;
int altitude;
public Place(int latitude, int longitude, int altitude) {
this.latitude = latitude;
this.longitude = longitude;
this.altitude = altitude;
}
public void changePlace(int latitude, int longitude, int altitude) {
this.latitude += latitude;
this.longitude += longitude;
this.altitude += altitude;
}
}- 위와 같이 (제어자) (클래스와 동일한 이름) (매개변수) {}의 형식을 취한다.
- 그 후 괄호 안에 자신이 초기화 할 조건을 작성하면 된다.
5. this
this는 인스턴스 자기 자신을 가리키는 참조변수이다.
- 따라서 위의
this.latitude = latitude;와 같은 문장은 - 해당 인스턴스의 필드값인 this.latitude를 외부의 매개변수로 받은 latitude로 초기화시킨다. 라는 의미이다.
this()???
- this()는 생성자를 뜻한다. 아래의 코드 예시를 보자
Animal.java
package study.moon.test;
public class Animal {
String name;
Place place;
public Animal() {
this("animal",new Place(0,0,0));
}
public Animal(String name) {
this(name,new Place(0,0,0));
}
public Animal(String name, Place place) { //<------생성자
this.name = name;
this.place = place;
}
public void move(int latitude, int longitude, int altitude) {
place.changePlace(latitude,longitude,altitude);
}
}- 위에서 볼 수 있는 예시와 같이 this(...) 을 사용하여 클래스 내부에 선언한 생성자 메소드를 불러올 수 있다.
6. 이진트리란?

각각의 노드가 최대 두 개의 자식 노드를 가지는
트리 자료구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드 라고 한다.
그렇다면 우리는 왜 이진트리를 사용할까?
- 아래의 그림을 보자.


- 위의 그림을 보면 일반적인 정렬된 선형자료구조의 탐색보다 이진트리를 활용한 이진탐색트리가 월등하게 탐색 시간이 짧은 것을 확인할 수 있다.
- 트리자료구조는 탐색에 걸리는 시간이 O(log n) 인 반면 선형 자료구조는 탐색에 걸리는 시간이 O(n)이다.
7. 이진트리 구현하기
1.int 값을 가지고 있는 이진트리를 나타내는 Node 클래스를 정의한다.
2.Node 클래스는 int value, Node left, Node right를 필드로 가지고 있어야 한다.
(2-1) 추가적으로 parnet노드를 필드에 넣으면 이진트리를 활용한 다른 로직을 확장하기에 훨씬 편리할 것 같다.
3.BinaryTree라는 클래스를 정의하고 주어진 노드를 기준으로 출력하는 bfs(Node node)와, dfs(Node node)를 구현한다.
4.dfs(Node node)는 왼쪽 - 루트 - 오른쪽 순으로 순회한다.
Node.java
package issue5;
public class Node {
int value;
Node parent;
Node left;
Node right;
public Node(int value, Node parent) {
this.value = value;
this.parent = parent;
}
public void addLeft(int value) {
this.left = new Node(value,this);
}
public void addRight(int value) {
this.right = new Node(value,this);
}
}BinaryTree.java
package issue5;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class BinaryTree {
Node root;
private final List<Integer> dfsResult = new ArrayList<>();
private final List<Integer> bfsResult = new ArrayList<>();
public BinaryTree() {
}
public void init(int value) {
root = new Node(value, null);
}
public List<Integer> getDFSResult() {
dfsResult.clear();
dfs(root);
return dfsResult;
}
public List<Integer> getBFSResult() {
bfsResult.clear();
bfs(root);
return bfsResult;
}
private void dfs(Node node) {
if (node.left == null) {
dfsResult.add(node.value);
return;
}
dfs(node.left);
dfsResult.add(node.value);
if (node.right == null) {
dfsResult.add(node.value);
System.out.println(node.value);
}
dfs(node.right);
}
private void bfs(Node node) {
LinkedList<Node> queue = new LinkedList<>();
queue.add(node);
while (!queue.isEmpty()) {
Node poll = queue.poll();
bfsResult.add(poll.value);
if (poll.left != null) {
queue.add(poll.left);
}
if (poll.right != null) {
queue.add(poll.right);
}
}
}
}BinaryTreeTest
package issue5;
import static org.junit.jupiter.api.Assertions.*;
import java.util.ArrayList;
import java.util.List;
import org.junit.jupiter.api.BeforeEach;
import org.junit.jupiter.api.Test;
class BinaryTreeTest {
BinaryTree tree;
@BeforeEach
void init() {
tree = new BinaryTree();
tree.init(50);
tree.root.addLeft(60);
tree.root.addRight(70);
tree.root.left.addLeft(80);
tree.root.left.addRight(90);
tree.root.right.addLeft(100);
tree.root.right.addRight(110);
}
@Test
void test_binary_tree_dfs() {
List<Integer> list = new ArrayList<>();
list.add(80);
list.add(60);
list.add(90);
list.add(50);
list.add(100);
list.add(70);
list.add(110);
List<Integer> result = tree.getDFSResult();
for (int i = 0; i < list.size(); i++) {
assertEquals(list.get(i),result.get(i));
}
}
@Test
void test_binary_tree_bfs() {
List<Integer> list = new ArrayList<>();
list.add(50);
list.add(60);
list.add(70);
list.add(80);
list.add(90);
list.add(100);
list.add(110);
List<Integer> result = tree.getBFSResult();
for (int i = 0; i < list.size(); i++) {
assertEquals(list.get(i),result.get(i));
}
}
}BinarySearchTree 구현하기
-
위에 작성한 이진트리는 일일이 하나씩 데이터를 삽입하고 탐색해야한다. 그 결과 api 편의성도 부족하고 이진트리의 장점이 전혀 나타나질 않는다.
-
따라서 위에 보았던 그림에서와 같은 이진트리의 유용함을 살리기 위해 이진탐색트리 를 구현해보자.
-
자료구조에 당연히 있어야 할 remove와 contains 도 추가 로 메소드를 작성해보자.
-
반복문과 재귀 를 둘다 사용하여 구현해보자.
BinarySearchTree.java
package issue5;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class BinarySearchTree {
private Node node;
private final List<Integer> dfsResult = new ArrayList<>();
private final List<Integer> bfsResult = new ArrayList<>();
public BinarySearchTree() {
}
//recursive
public void add(int value) {
if (node == null) {
node = new Node(value, null);
return;
}
Node result = find(node, value);
if (result.value == value) {
System.out.println("tree has this value already.");
} else {
if (result.value > value) {
result.addLeft(value);
} else {
result.addRight(value);
}
}
}
//iter
// public void add(int value) {
// Node tmp = node;
// if (node == null) {
// node = new Node(value, null);
// return;
// }
// while (true) {
// if (tmp.value > value) {
// if (tmp.left == null) {
// tmp.addLeft(value);
// break;
// }
// tmp = tmp.left;
// } else if (tmp.value < value) {
// if (tmp.right == null) {
// tmp.addRight(value);
// break;
// }
// tmp = tmp.right;
// } else {
// System.out.println("tree has this value already.");
// }
// }
// }
public void remove(int value) {
if (node == null) {
System.out.println("tree hasn't any value");
return;
}
Node result = find(node, value);
if (result.parent==null) {
Node near = getNear(result);
if (near.parent == null) {
node = null;
return;
}
result.value = near.value;
if (near.left!=null && near.right==null) {
Node parent = near.parent;
if (parent.value > value) {
parent.left = near.left;
} else {
parent.right = near.left;
}
}
if (near.left==null && near.right!=null) {
Node parent = near.parent;
if (parent.value > value) {
parent.left = near.right;
} else {
parent.right = near.right;
}
}
near.parent = null;
return;
}
if (result.value == value) {
if (result.left == null && result.right == null) {
Node parent = result.parent;
if (parent.value > value) {
parent.left = null;
} else {
parent.right = null;
}
result.parent = null;
}
if (result.left != null && result.right == null) {
Node parent = result.parent;
if (parent.value > value) {
parent.left = result.left;
} else {
parent.right = result.left;
}
result.parent = null;
}
if (result.left == null && result.right != null) {
Node parent = result.parent;
if (parent.value > value) {
parent.left = result.right;
} else {
parent.right = result.right;
}
result.parent = null;
}
if (result.left != null && result.right != null) {
Node near = getNear(result);
result.value = near.value;
Node parent = near.parent;
if (parent.value > value) {
parent.left = null;
} else {
parent.right = null;
}
near.parent = null;
}
} else {
System.out.println("tree hasn't this value");
}
}
//recursive
public boolean contains(int value) {
if (node == null) {
return false;
}
Node result = find(this.node, value);
return result.value == value;
}
//iter
// public boolean contains(int value) {
// if (node == null) {
// return false;
// }
// Node tmp = node;
// while (true) {
// if (tmp.value > value) {
// if (tmp.left == null) {
// return false;
// }
// tmp = tmp.left;
// } else if (tmp.value < value) {
// if (tmp.right == null) {
// return false;
// }
// tmp = tmp.right;
// } else {
// return true;
// }
// }
// }
private Node find(Node node, int value) {
if (node.value > value) {
if (node.left == null) {
return node;
}
return find(node.left, value);
} else if (node.value < value) {
if (node.right == null) {
return node;
}
return find(node.right, value);
} else {
return node;
}
}
private Node getNear(Node node) {
if (node.left!=null) {
node = node.left;
while(node.right!=null) {
node = node.right;
}
}else if (node.right!=null) {
node = node.right;
while(node.left!=null) {
node = node.left;
}
}
return node;
}
public List<Integer> getDFSResult() {
dfsResult.clear();
dfs(node);
return dfsResult;
}
public List<Integer> getBFSResult() {
bfsResult.clear();
bfs(node);
return bfsResult;
}
private void dfs(Node node) {
if (node.left == null) {
dfsResult.add(node.value);
return;
}
dfs(node.left);
dfsResult.add(node.value);
if (node.right == null) {
dfsResult.add(node.value);
}
dfs(node.right);
}
private void bfs(Node node) {
LinkedList<Node> queue = new LinkedList<>();
queue.add(node);
while (!queue.isEmpty()) {
Node poll = queue.poll();
bfsResult.add(poll.value);
if (poll.left != null) {
queue.add(poll.left);
}
if (poll.right != null) {
queue.add(poll.right);
}
}
}
}BinarySearchTreeTest.java
package issue5;
import static org.junit.jupiter.api.Assertions.*;
import java.util.ArrayList;
import java.util.List;
import org.junit.jupiter.api.BeforeEach;
import org.junit.jupiter.api.Test;
class BinarySearchTreeTest {
BinarySearchTree tree;
@BeforeEach
void init() {
tree = new BinarySearchTree();
tree.add(50);
tree.add(30);
tree.add(70);
tree.add(20);
tree.add(40);
tree.add(60);
tree.add(80);
}
@Test
void test_binary_search_tree_bfs() {
List<Integer> expects = new ArrayList<>();
expects.add(50);
expects.add(30);
expects.add(70);
expects.add(20);
expects.add(40);
expects.add(60);
expects.add(80);
List<Integer> bfsResult = tree.getBFSResult();
for (int i = 0; i < expects.size(); i++) {
assertEquals(expects.get(i),bfsResult.get(i));
}
}
@Test
void test_binary_search_tree_dfs() {
List<Integer> expects = new ArrayList<>();
expects.add(20);
expects.add(30);
expects.add(40);
expects.add(50);
expects.add(60);
expects.add(70);
expects.add(80);
List<Integer> dfsResult = tree.getDFSResult();
for (int i = 0; i < expects.size(); i++) {
assertEquals(expects.get(i),dfsResult.get(i));
}
}
@Test
void test_binary_search_tree_contains() {
assertTrue(tree.contains(20));
assertTrue(tree.contains(30));
assertTrue(tree.contains(40));
assertTrue(tree.contains(50));
assertTrue(tree.contains(60));
assertTrue(tree.contains(70));
assertTrue(tree.contains(80));
assertFalse(tree.contains(15));
assertFalse(tree.contains(25));
assertFalse(tree.contains(0));
}
@Test
void test_binary_search_tree_remove() {
tree.remove(20);
tree.remove(40);
tree.remove(50);
tree.remove(60);
tree.remove(80);
assertFalse(tree.contains(20));
assertTrue(tree.contains(30));
assertFalse(tree.contains(40));
assertFalse(tree.contains(50));
assertFalse(tree.contains(60));
assertTrue(tree.contains(70));
assertFalse(tree.contains(80));
}
}균형잡힌 이진탐색트리
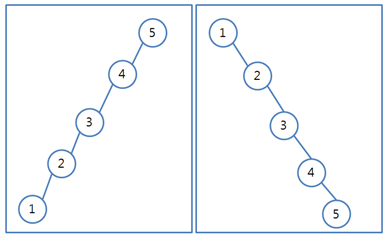
- 이진탐색트리의 문제점은 무엇일까? 다음의 그림을 보자
-
다음과 같이 편향된 상태의 이진탐색트리가 계속된다면 데이터의 탐색 수행시간이 O(log n)이 아니라 O(n)에 가까워질 것이다.
-
따라서 편향된 이진탐색트리의 균형을 잡아주는 것이 필요하다.
-
균형잡힌 이진탐색트리의 종류중 가장 유명한 것은 AVL Tree , Red-Black Tree가 있다.
AVL Tree

Red-Black Tree


-
위의 방법을 사용하여 균형잡힌 이진탐색트리를 구성면 원하는 데이터를 검색할 때 WorstCase의 시간복잡도를 최소한으로 줄일 수 있다.
-
참고로 자바에서 사용하는 Tree는 Red-Black Tree 기반이다.

힙
-
heap 자료구조를 사용하여 자료내에서 최댓값과 최솟값을 빠르게 찾아낼 수 있다.
-
완전 이진트리를 사용한 자료구조이다. 부모노드는 항상 자식 노드보다 우선순위에 있게된다.

- 자바에서는 다음의 heap자료구조를
PriorityQueue<T>라는 이름으로 구현해 놓았다.
'Java&Spring > STUDY HALLE' 카테고리의 다른 글
| [Java] 패키지 (0) | 2020.12.29 |
|---|---|
| [Java] 상속 (0) | 2020.12.22 |
| [Java] 선형 자료구조 (0) | 2020.12.07 |
| [Java] GitHub Library 사용법 (0) | 2020.12.06 |
| [Java] JUnit5 (0) | 2020.12.05 |